Definitie:
Fie G=(V, M) un graf neorientat. Graful G se numeşte graf complet, dacă oricare două vârfuri distincte ale sale sunt adiacente.
Exemplu de graf neorientat complet:
G=(V, M) unde: V={ 1,2,3,4} si M={[1,2], [1,3], [l,4], [2,3], [2,4], [3,4]}
Reprezentarea sa grafică este:

Observatii:
- Într-un graf complet cu n vârfuri gradul fiecărui vârf este n-1, deoarece fiecare vârf este legat prin
muchii de toate celelalte vârfuri. - Graful complet cu n vârfuri se notează cu Kn.
În particular, graful:
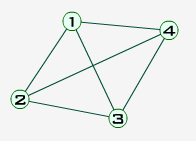
se notează K4 (este un graf complet cu 4 vârfuri).
Propozitie:
Într-un graf complet cu n vârfuri, notat Kn, există n(n-1)/2 muchii.