Numim poligon drept un poligon cu laturile consecutive perpendiculare și lungimile laturilor numere naturale nenule. Un poligon drept cu n laturi este descris de un șir de n numere întregi nenule în care lungimile laturilor sunt date de valoarea absolută a numerelor din șir, iar semnul precizează poziția laturilor, un număr pozitiv însemnând latură spre dreapta sau în sus față de extremitatea laturii precedente, iar un număr negativ însemnând latură în jos sau spre stânga față de extremitatea laturii precedente; de exemplu șirul 1, 1, -1, -1 reprezintă un pătrat de latură 1 (prima latură spre dreapta, a doua în sus, a treia spre stânga, a patra în jos). Vom considera laturile ca fiind orizontale sau verticale, prima latură enumerată fiind orizontală spre dreapta, dacă numărul este pozitiv, sau spre stânga, dacă numărul este negativ.
Cerința
Se dau unul sau mai multe șiruri de numere întregi nenule.
1. Să se stabilească, pentru fiecare dintre ele, dacă reprezintă un poligon drept.
2. Știind că șirurile date reprezintă poligoane drepte, să se determine aria fiecăruia.
Date de intrare
Fișierul de intrare drept.in conține pe prima linie, separate prin spațiu, un număr natural C și un număr natural T. Următoarele 2 * T linii vor descrie testele, câte două linii pentru fiecare test. Pe prima linie corespunzătoare unui test se află un număr natural n, iar pe a doua linie un șir de n numere întregi, separate prin câte un spațiu.
Date de ieșire
Fișierul de ieșire drept.out va conține pe o singură linie rezultatele corespunzătoare celor T teste, separate prin câte un spațiu. Dacă C = 1 pentru fiecare șir rezultatul este 1, dacă acesta reprezintă un poligon drept, sau 0 altfel. Dacă C = 2 pentru fiecare șir rezultatul este aria poligonului drept corespunzător.
Restricții și precizări
1 ≤ T ≤ 104 ≤ n ≤ 100- Pentru teste în valoare de
45de puncteC = 1, pentru restul de55de puncteC = 2 - Pentru teste în valoare de
30de puncteC = 1și numerele ce descriu figura sunt întregi nenule aparținând intervalului[-100, 100] - Pentru celelalte
15puncte șiC = 1numerele ce descriu figura sunt întregi nenule aparținând intervalului[-1.000.000.000, 1.000.000.000] - Pentru teste în valoare de
33de puncte se garantează că avemC = 2și intersecția dintre orice orizontală cu poligonul este fie vidă, fie formată dintr-un singur segment. - Pentru testele în care valoarea lui
Ceste2, numerele din șirul ce descrie poligonul sunt întregi nenule din intervalul[-100, 100]și se garantează că aceste șiruri reprezintă poligoane drepte. - Într-un poligon drept laturile nu au puncte comune, exceptând capetele laturilor adiacente.
- Prima și ultima latură ale unui poligon drept sunt perpendiculare.
Exemplul 1:
drept.in
1 2 8 5 3 -3 -1 2 -1 -4 -1 8 -2 1 3 1 -4 -3 2 1
drept.out
1 0
Explicație
Șirurile descriu următoarele figuri:
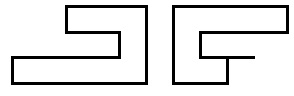
Exemplul 2:
drept.in
2 2 8 5 3 -3 -1 2 -1 -4 -1 4 1 1 -1 -1
drept.out
9 1
#include <fstream>
#include <iostream>
using namespace std;
struct punct {
int x;
int y;
};
punct v[210];
int C, t, n, xmin, xmax, ymin, ymax, i, d, j, k;
int poligon, aria, jos, stanga;
int punctPeSegment(int i, int j) {
if (v[i].x >= min(v[j].x, v[j+1].x) && v[i].x <= max(v[j].x, v[j+1].x))
if (v[i].y >= min(v[j].y, v[j+1].y) && v[i].y <= max(v[j].y, v[j+1].y))
return 1;
return 0;
}
int intersectieSegmente(punct a, punct b, punct c, punct d) {
punct aux;
if (a.x > b.x) {
aux = a;
a = b;
b = aux;
}
if (c.y > d.y) {
aux = c;
c = d;
d = aux;
}
if ((c.y - a.y) * 1LL * (d.y - a.y) <= 0)
if ((c.x - a.x) * 1LL * (c.x - b.x) <= 0)
return 1;
return 0;
}
int main () {
ifstream fin ("drept.in");
ofstream fout("drept.out");
fin>>C>>t;
for (;t--;) {
fin>>n;
xmin = xmax = ymin = ymax = 0;
v[0].x = 0;
v[0].y = 0;
for (i=1;i<=n;i++) {
fin>>d;
if (i%2 == 1) {
v[i].x = v[i-1].x + d;
v[i].y = v[i-1].y;
} else {
v[i].x = v[i-1].x;
v[i].y = v[i-1].y + d;
}
xmin = min(xmin, v[i].x);
xmax = max(xmax, v[i].x);
ymin = min(ymin, v[i].y);
ymax = max(ymax, v[i].y);
}
poligon = 1;
if (v[n].x != 0 || v[n].y != 0)
poligon = 0;
for (i=0;i<n-1;i++) {
for (j=i+2;j<n;j++) {
if (i == 0 && j == n-1)
continue;
if (i%2 == j%2) {
/// paralele
if (punctPeSegment(i, j))
poligon = 0;
if (punctPeSegment(i+1, j))
poligon = 0;
if (punctPeSegment(j, i))
poligon = 0;
if (punctPeSegment(j+1, i))
poligon = 0;
} else {
if (i%2 == 0) {
if (intersectieSegmente(v[i], v[i+1], v[j], v[j+1]))
poligon = 0;
} else {
if (intersectieSegmente(v[j], v[j+1], v[i], v[i+1]))
poligon = 0;
}
}
}
}
if (C!=1) {
aria = 0;
for (i=xmin+1;i<=xmax;i++)
for (j=ymin+1;j<=ymax;j++) {
jos = 0;
stanga = 0;
for (k=0;k<n;k++) {
if (k%2 == 1) {
if (v[k].x < i && min(v[k].y, v[k+1].y) < j && max(v[k].y, v[k+1].y) >= j)
stanga++;
} else {
if (v[k].y < j && min(v[k].x, v[k+1].x) < i && max(v[k].x, v[k+1].x) >= i)
jos++;
}
}
if (stanga % 2 && jos % 2)
aria++;
}
}
if (C == 1) {
fout<<poligon<<" ";
} else {
fout<<aria<<" ";
}
}
return 0;
}