Definitie.
Fie G=(V, M) un graf neorientat. Se numeşte graf partial, al grafului G, graful neorientat G1=(V, M1) unde M1 ⊆ M.
Concluzie:
Un graf partial al unui graf neorientat G=(V, M) are aceeaşi multime de vârfuri ca şi G iar multimea muchiilor este o submultime a lui M sau chiar M.
Exemplu:
Fie graful neorientat: G=(V, M) unde: V={ 1,2,3,4} si M={[1,2], [1,4], [2,3]}
- Un exemplu de graf partial al grafului G este graful neorientat:
G1=(V, M,) unde: V={1,2,3,4} M1={[1,2],[1,4]} (s-a eliminat muchia [2,3]) reprezentat grafic astfel:
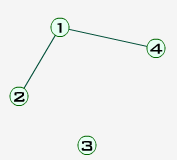
- Un exemplu de graf partial al grafului G este graful neorientat:
G1=(V,M1) unde: V={1,2,3,4} M1= (s-au eliminat toate muchiile) reprezentat grafic astfel:

Observatie:
Fie G=(V, M) un graf neorientat. Un graf partial, al grafului G, se obtine păstrând vârfurile şi eliminând eventual nişte muchii (se pot elimina şi toate muchiile, sau chiar nici una).