Definiţie: Se numeşte lanţ L = [x0, x1, …, xn]o succesiune de vârfuri cu proprietatea că oricare
două vârfuri consecutive sunt adiacente.
Vârfurile x0 şi xn se numesc extremităţile lanţului. Numărul n se numeşte lungimea lanţului şi
este numărul de muchii din care este format.
Lanţul care conţine numai vârfuri distincte, două câte două, este lanţ elementar.
Lanţul care conţine numai muchii distincte este lanţ simplu. Dacă muchiile unui lanţ nu sunt
distincte se numeşte lanţ compus.
O matrice pătratică de ordin n se numeşte matricea lanţurilor, dacă:

Exemplu: Fie G = (X, U), a.î. X = {1, 2, 3, 4, 5, 6}, iar
U = {[1, 2], [2, 3], [3, 4], [3, 5], [4, 5], [5, 6]}.
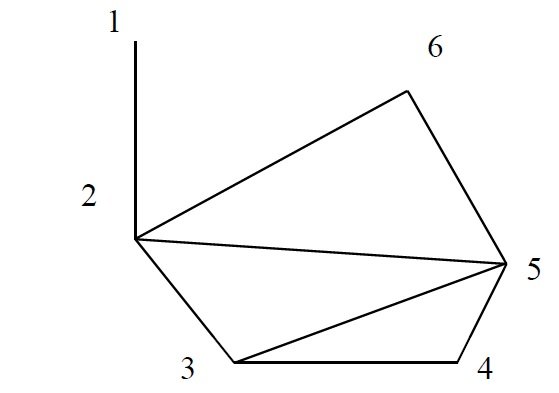
Lanţul 2, 3, 5, 6 este simplu şi elementar de lungime 3.
Lanţul 5, 3, 4, 5, 6 este simplu, dar nu este elementar de lungime 4.
Lanţul 5, 3, 4, 5, 3, 2 este compus şi nu este elementar de lungime 5.
Definiţie: Un lanţ pentru care x0 = xn (primul nod coincide cu ultimul) se numeşte ciclu. Dacă
toate vârfurile unui ciclu, cu excepţia primului şi ultimului, sunt distincte, ciclul se numeşte
elementar.
Lungimea unui ciclu nu poate fi 2.
Un ciclu se numeşte par dacă lungimea sa este pară şi impar în caz contrar.
Exemplu: În graful din figura anterioară lanţul 3, 4, 5, 3 este un ciclu elementar impar. Lanţul 2, 5,
3, 4, 5, 6, 2 este un ciclu par, dar nu este elementar.