Se consideră A un tablou bidimensional cu n linii, n coloane și elemente numere naturale. O zonă triunghiulară a tabloului, reprezentată de tripletul (lin, col, k), este o zonă de forma unui triunghi dreptunghic cu catetele de lungime egală cu |k|, definită astfel:

1. Pentru k>0, zona este compusă din k linii:
   • pe prima linie a zonei se află elementele A[lin][col], A[lin][col+1], …, A[lin][col+k-1];
   • pe a doua linie a zonei se află elementele A[lin+1][col], A[lin+1][col+1], …, A[lin+1][col+k-2];
   • pe a treia linie a zonei se află elementele A[lin+2][col], A[lin+2][col+1], …, A[lin+2][col+k-3];
   • …
   • pe ultima linie a zonei se află elementul A[lin+k-1][col].
2. Pentru k<0, zona este compusă din |k|=-k linii:
   • pe prima linie a zonei se află elementul A[lin-|k|+1][col];
   • pe a doua linie a zonei se află elementele A[lin-|k|+2][col-1], A[lin-|k|+2][col];
   • …
   • pe ultima linie a zonei se află elementele A[lin][col-|k|+1], A[lin][col-|k|+2],…, A[lin][col].

Suma elementelor ce compun o zonă triunghiulară se numește suma zonei.

Cerința

Scrieţi un program care, cunoscând tabloul A şi Q zone triunghiulare, determină cea mai mare dintre sumele zonelor.

Date de intrare

Fișierul de intrare triunghi.in conține pe prima linie numărul natural n, cu semnificaţia din enunţ. Pe următoarele n linii se găsesc câte n valori naturale, reprezentând elementele tabloului A. Pe linia n+2 se află numărul natural Q, reprezentând numărul zonelor triunghiulare. Pe următoarele Q linii se găsesc tripletele de valori lin col k, care reprezintă cele Q zone, în forma descrisă în enunţ. Valorile aflate pe aceeaşi linie a fişierului sunt separate prin câte un spațiu.

Date de ieșire

Fișierul de ieșire triunghi.out va conține o singură linie pe care va fi scris un număr natural reprezentând suma maximă cerută.

Restricții și precizări

• 3 ≤ n ≤ 1000; 1 ≤ Q ≤ 100000; 2 ≤ |k| ≤ n
• Valorile din tablou sunt numere naturale din intervalul [1,100].
• Liniile şi coloanele tabloului A sunt numerotate de la 1 la n (liniile de sus în jos, iar coloanele de la stânga la dreapta).
• |k| reprezintă modulul numărului k (k, pentru k≥0, respectiv -k, pentru k<0).
• Se garantează că orice zonă triunghiulară dintre cele Q este complet inclusă în tabloul A.

Exemplu

triunghi.in

6
5 8 10 4 9 4
2 10 10 2 4 8
8 10 3 4 6 6
4 6 9 7 1 9
6 7 2 2 10 6
10 4 6 1 10 4
3
4 1 3
4 4 -4
6 5 -2

triunghi.out

59

Explicație

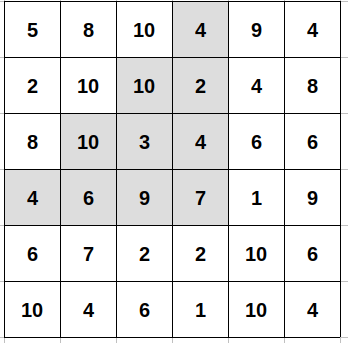
Zona triunghiulară de sumă maximă (59) este reprezentată de tripletul (4 4 -4) și conține
valorile evienţiate: 59=4+(10+2)+(10+3+4)+(4+6+9+7).

#include <fstream>
#define NMAX 1002

using namespace std;
ifstream fin("triunghi.in");
ofstream fout("triunghi.out");
int n, Q;
int A[NMAX][NMAX];
int sl[NMAX][NMAX];//sl[i][j]=suma elementele de pe linia i de la 1 la j
int sd[NMAX][NMAX];//sd[i][j]=suma elem din dreptunghiul cu colutl 1,1 si coltul i,j
int st[NMAX][NMAX];//st[i][j] este suma elementelor din trapezul cu baza mare pe linia 1
//si baza mica pe linia i de la 1 la j
int smax;
int detsuma(int lin, int col, int k);
int main()
{int i, j, lin, col, k, t, suma;
 fin>>n;
 for (i=1; i<=n; i++)
     for (j=1; j<=n; j++)
         {
          fin>>A[i][j];
          sl[i][j]=sl[i][j-1]+A[i][j];
          sd[i][j]=sd[i-1][j]+sd[i][j-1]-sd[i-1][j-1]+A[i][j];
          if (j==n) st[i][j]=sd[i][j]; else st[i][j]=st[i-1][j+1]+sl[i][j];
          }

 fin>>Q;
 for (t=0; t<Q; t++)
     {
      fin>>lin>>col>>k;
      if (k>0)
          suma=detsuma(lin,col,k);
          else
          suma=sd[lin][col]-sd[lin][col+k]-sd[lin+k][col]+sd[lin+k][col+k]-detsuma(lin+k+1,col+k+1,-k-1);
      if (suma>smax) smax=suma;
     }
 fout<<smax<<'\n';
 fout.close();
 return 0;
}


int detsuma(int lin, int col, int k)
{
 if (col+k-1==n)
    return st[lin+k-1][col]-sd[lin+k-1][col-1]-sd[lin-1][col+k-1]+sd[lin-1][col-1];
 return    st[lin+k-1][col]-sd[lin+k-1][col-1]-st[lin-1][col+k]  +sd[lin-1][col-1];
}