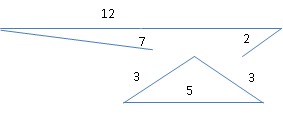
Gigel este un pasionat al triunghiurilor. El colectează beţişoare de diferite lungimi şi le asamblează în diferite triunghiuri. Ieri, el avea 6 beţişoare de lungimi 5, 2, 7, 3, 12 şi 3. Din aceste bețișoare, Gigel a construit un triunghi de laturi 3, 3 şi 5, iar beţişoarele de lungimi 2, 7, 12 au rămas nefolosite pentru că aceste lungimi nu pot forma laturile unui triunghi.
Din acest motiv, Gigel s-a hotărât să facă o colecţie de beţişoare, dintre care oricum ar alege 3 elemente, acestea să nu poată forma laturile unui triunghi, proprietate pe care o vom numi în continuare proprietate anti-triunghi. Gigel, pornind de la setul iniţial de lungimi 2, 7, 12, s-a gândit la două metode de realizare a unei colecţii de 5 beţişoare cu proprietatea anti-triunghi, şi anume:
1.Păstrează cel mai scurt beţişor, cel de lungime 2, şi creează un set nou adăugând alte beţişoare de lungime mai mare sau egală cu cel iniţial. De exemplu, următoarele 5 lungimi sunt corecte: 2, 2, 12, 50, 30.
2.Păstrează toate beţişoarele, şi anume 2, 7,12, pe care le va completa cu alte beţişoare de diferite lungimi (mai scurte sau mai lungi), astfel ca proprietatea anti-triunghi să se păstreze. Următoarele 5 lungimi respectă proprietatea anti-triunghi: 2, 7, 12, 4, 1.
Cerinţă
Cunoscând un şir de n numere naturale nenule a1, a2, …, an având proprietatea anti-triunghi, şi un număr k (k>n), se cere să construiţi un şir de k numere naturale având proprietatea anti-triunghi, în conformitate cu una dintre următoarele două restricţii:
Varianta 1. Cel mai mic element este identic cu cel mai mic element din şirul iniţial.
Varianta 2. Printre cele k elemente ale şirului construit se regăsesc toate elementele şirului iniţial.
Date de intrare
Fişierul de intrare triunghi2.in conţine pe prima linie valorile numerelor v, n şi k, separate prin spaţiu. Linia următoare conţine n numere naturale separate prin spaţiu, ce formează un şir cu proprietatea anti-triunghi.
Date de ieşire
Fişierul de ieşire triunghi2.out va conţine k numere pe o singură linie.
Dacă valoarea lui v este 1, atunci fişierul va conţine k numere naturale cu proprietatea anti-triunghi, separate prin spaţiu, în care cel mai mic element este identic cu minimul şirului dat în fişierul de intrare.
Dacă valoarea lui v este 2, atunci fişierul va conţine k numere naturale cu proprietatea anti-triunghi, separate prin spaţiu, printre care se regăsesc toate elementele şirului iniţial.
Restricţii şi precizări
3 ≤ n < k ≤ 46;1 ≤ lungimea unui beţişor ≤ 2.000.000.000;- Pentru rezolvarea corectă a primei cerinţe se acordă
30de puncte, iar pentru cerinţa a doua se acordă70de puncte; - Se garantează că întotdeauna există soluţie;
- Soluţia nu este unică – se admite orice răspuns corect.
Exemple
triunghi2.in
1 3 5 7 2 12
triunghi2.out
2 2 30 50 12
triunghi2.in
2 3 5 7 2 12
triunghi2.out
1 4 12 7 2
Explicație
Pentru primul exemplu:
v=1, n=3, k=5. În varianta 1 avem de tipărit 5 numere, valoarea minimului este 2 în ambele şiruri.
Pentru al doilea exemplu:
v=2, n=3, k=5. În varianta 2 printre elementele şirului tipărit se regăsesc toate elementele şirului iniţial.
SOLUTIE 1
#include <fstream>
using namespace std;
int ok[50];
int main()
{ int pa,pb,a[50],n,k,i,j,b[50],aux,x,opt;
ifstream fin("triunghi2.in");
ofstream fout("triunghi2.out");
fin>>opt>>n>>k;
for (i=1;i<=n;i++)
fin>>a[i];
for (i=1;i<n;++i)
for (j=i+1;j<=n;++j)
if (a[i]>a[j])
{
aux=a[i];
a[i]=a[j];
a[j]=aux;
}
if (opt==1)
{
b[1]=b[2]=a[1];
for (i=3;i<=k;i++)
b[i]=b[i-1]+b[i-2];
for (i=1;i<=k;++i)
fout<<b[i]<<' ';
fout<<"\n";
}
else
{
if (a[1]==a[2])
{
b[1]=b[2]=a[1];
ok[1]=ok[2]=1; //in sirul b bifam toate elementele
pa=3; // ce apartin lui a
}
else
{
b[1]=b[2]=1;
if (a[1]==1) // se bifeaza elementul 1 in cazul
{
ok[1]=1; // in care este element din a
pa=2;
}
else
pa=1;
}
pb=2;
while (pa<n)
{
x=b[pb]+b[pb-1];
if (b[pb]+x<=a[pa] && x<=a[pa+1]-a[pa])
b[++pb]=x;
else
{
b[++pb]=a[pa++];
ok[pb]=1;
}
}
while (pa==n)
{
x=b[pb]+b[pb-1];
if(b[pb]<=a[pa]-x)
b[++pb]=x;
else
{
b[++pb]=a[pa++];
ok[pb]=1;
}
}
while (b[pb]<=2000000000-b[pb-1])
{
b[pb+1]=b[pb]+b[pb-1];
pb++;
}
for (i=1;i<=pb;i++)
if (ok[i]) fout<<b[i]<<" ";
x=k-n;
for(i=1;x && i<=pb;i++)
if (!ok[i])
{
fout<<b[i]<<" ";
--x;
}
fout<<"\n";
}
fin.close();
fout.close();
return 0;
}
SOLUTIE 2
#include <iostream>
#include <fstream>
using namespace std;
ifstream f("triunghi2.in");
ofstream g("triunghi2.out");
int n,k,m,choise;//m-valoarea minima din vector
int nr;//numarul de bete adaugate
int v[50], u[50]; //v - initial, u-dupa adaugare
void citire(){
int i;
f>>choise>>n>>k;
m=2000000000;
for(i=1;i<=n;i++){
f>>v[i];//citesc betioasere si calculez valoarea minima
if(v[i]<m) m=v[i];
u[i]=v[i];//pun toate betele in solutie pt. pct. b
}
}
void solutie1(){
int b1,b2,b3;
g<<m<<" "<<m<<" ";//afisez cel mai mic bat de doua ori
nr=2;//am doua bete
b1=b2=m;
while(nr<k) {//cat timp nu am k bete adaugate
b3=b2+b1;//calculez urmatoarea lungime cu care nu pot forma triunghi
b1=b2;b2=b3;//trec la urmatoarele 2 bete
g<<b2<<" ";//afisez lungimea noului bat
nr++;//contabilizez batul
}
g<<"\n";
}
void sortare(){//sortez betele initiale
int i,j,aux;
for(i=1;i<n;i++)
for(j=i+1;j<=n;j++)
if(v[i]>v[j]) {aux=v[i];v[i]=v[j];v[j]=aux;}
}
void solutie2(){
//incerc sa pun bete inainte de fiecare bat i cu i<-1,n
int i,b1,b2,b3,j;//b1-penultimul bat pus, b2 - ultimul bat pus, b3 - noul bat care se adauga
i=1;//incepand cu primul bat din stiva initiala
nr=n;//am cele n bete initiale
b1=0;//penultimul bat pus
b2=1;//ultimul bat pus
if(b1+b2+v[i]>v[i+1]){//daca adaug batul de lungime 1 pot depasi al doilea in cazul 2 2 5 7
b1=v[i];b2=v[i+1]; //atunci incep cu cele mai mici 2 bete
}
else {//altfel adaug batul de lungime 1
nr = nr + 1;
u[nr]=1;
}
//incerc sa pun bete inainte de batul v[i]
while(nr<k && i<=n) { //cat timp nu am pus k bete si mai sunt bete inainte carora pot pune
b3=b2+b1;//incerc sa pun b3
if(b3+b2<=v[i]){//daca suma dintre ultimul bat adaugat si nnoul bat e ok
nr++;//creste numarul de bete adaugate
u[nr]=b3;//retin noul bat
b1=b2;//penultimul bat
b2=b3;//ultimul bat
}
else {//nu mai pot pune bete inainte de v[i]
b1=b2;//penultimul bat adaugat
b2=v[i];//ultimul bat
i=i+1;//trec la urmatorul bat inaintea caruia incerc sa pun
}
}
if(nr<k){//daca nu am pus toate betele inainte de betele initiale
//pun bete dupa ultimul bat
if(v[n-1]>u[nr])b1=v[n-1];//verific care e penultimul element
else b1=u[nr];
b2=v[n];
while(nr<k) {
b3=b2+b1;
nr++;
u[nr]=b3;
b1=b2;
b2=b3;
}
}
for(i=1;i<=k;i++)
g<<u[i]<<" ";
}
int main()
{
citire();
if(choise==1)
solutie1();
else {
sortare();
solutie2();
}
return 0;
}