Definitie:
Fie G =(V, M) un graf bipartit. Graful G se numeşte graf bipartit complet, dacă pentru orice x din V1 şi orice y din V2 exista in G muchia [x,y].
Exemplu de graf neorientat bipartit:
G=(V, M) unde: V={ 1,2,3,4} si M={[1,3], [1,4], [2,3], [2,4]}
Reprezentarea sa grafică este:

Observatie 1:
A demonstra că un graf este bipartit complet înseamnă a demonstra :
-că este bipartit
– ca pentru orice x din Vl şi orice y din V2 există in G muchia [x,y].
Observatie 2:
Într-un graf bipartit complet în care V1 are p elemente şi V2 are q elemente există pq muchii.
Observatie 3:
Graful bipartit complet în care V1 are p elemente şi V2 are q elemente se notează cu Kp,q.
În particular, graful:
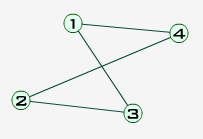
se notează K2,2 si este un graf bipartit complet cu |V1| = 2 şi |V2|=2.