Un fermier deține o fermă de formă dreptunghiulară cu lungimea m metri și lățimea n metri. Respectând principiul rotației culturilor, fermierul și a realizat un plan pentru semănarea culturilor în noul an. Astfel ,el a desenat un dreptunghi pe care l-a împărțit în m * n celule, fiecare corespunzând unui metru pătrat, și a colorat în culori diferite zonele care corespund unor culturi diferite. O cultură poate fi semănată pe mai multe parcele. Două celule care au o latură comună aparțin aceleiași parcele dacă au aceeași culoare (sunt însămânțate cu aceeași cultură). Fermierul are posibilitatea să irige o sigură parcelă și dorește să aleagă parcela cu cea mai mare suprafață. Nefiind mulțumit de suprafața rezultată, s-a întrebat dacă ar putea schimba cultura de pe o singură celulă, astfel încât să obțină o parcelă de suprafață mai mare.

Cerință

Dându-se dimensiunile fermei și pentru fiecare celulă culoarea corespunzătoare culturii semănate, determinați:

• Cerința 1: Suprafața maximă a unei parcele în planul inițial.
• Cerința 2: Numărul liniei, respectiv al coloanei celulei pe care va semăna o altă cultură și culoarea corespunzătoare noii culturi în vederea obţinerii celei mai mari parcele posibile.

Date de intrare

Fișierul de intrare ferma.in va conține:

• pe prima linie un număr natural v ( 1 ≤ v ≤ 2 ) indicând varianta cerinței de rezolvare;
• pe a doua linie două numere naturale m şi n separate printr-un spațiu, cu semnificația din enunț;
• pe fiecare dintre următoarele m linii se găsesc câte n caractere (litere mici), reprezentând codurile culturilor ce vor fi semănate pe cele n celule corespunzătoare fiecărei linii.

Date de ieşire

Fișierul de ieșire ferma.out va conține:

Cerința 1 – pentru v=1:

• pe prima linie numărul natural s, reprezentând suprafața maximă a unei parcele.

Cerința 2 – pentru v=2:

• pe prima linie două numere naturale separate printr-un spațiu, reprezentând numărul liniei, respectiv al coloanei celulei pe care va semăna o altă cultură, în vederea obținerii unei parcele cu suprafața maximă;
• pe a doua linie un caracter reprezentând codul culorii corespunzătoare noii culturi din celula determinată.

Restricţii şi precizări

• 2 ≤ m ≤ 400
• 2 ≤ n ≤ 400
• Numărul de culturi distincte este cel puţin 2 şi cel mult 26.
• 30% din teste vor avea pe prima linie valoarea 1, iar restul de 70% din teste vor avea pe prima linie valoarea 2.
• Pentru varianta 2 se punctează orice soluție care conduce la obținerea unei parcele cu suprafața maximă. Nu se acordă punctaje parțiale.

Exemple

ferma.in

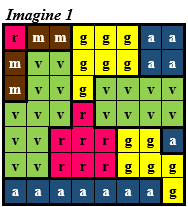
1
7 8
rmmgggaa
mvvgggaa
mvvgvvvv
vvvrvvvv
vvrrrgga
vvrrrggg
aaaaaaag

ferma.out

11

ferma.in

2
7 8
rmmgggaa
mvvgggaa
mvvgvvvv
vvvrvvvv
vvrrrgga
vvrrrggg
aaaaaaag

ferma.out

3 4
v

Explicație

Pentru primul exemplu:

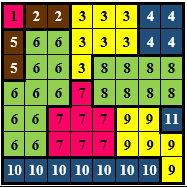
Datele corespund imaginilor de mai sus. Numerotarea parcelelor din imaginea 2 este utilizată pentru a simplifica explicațiile de mai jos și nu influențează datele problemei și nici algoritmul de rezolvare.

În varianta 1 se determină și se afișează suprafața maximă a unei parcele, care este egală cu 11 și corespunde parcelei 6, de culoare verde (codificată cu litera v în imaginea 1 şi în fişierul de intrare).

Pentru al doilea exemplu:

Pentru varianta 2:
Schimbând în verde (v) culoarea celulei de pe linia 3 şi coloana 4, se obține o parcelă cu suprafața 11+8+1=20 (se unesc parcelele cu numărul 6 respectiv 8).

O altă soluţie corectă este:
4 4
v

SOLUTIE

#include <fstream>

using namespace std;
ifstream fin ("ferma.in");
ofstream fout ("ferma.out");
int n, m, a[405][405], afill[405][405], nr, b[405*405], Max, ip, jp, cul, culoare, pa[405*405];

int xm[] = {-1, 1, 0, 0};
int ym[] = {0, 0, -1, 1};

bool OK(int i, int j) {
    if (i < 1 || j < 1 || i > n || j > m)
        return false;
    if (afill[i][j])
        return false;
    return true;
}

void algfill (int i, int j) {
    afill[i][j] = nr;
    b[nr]++;
    for (int l = 0; l < 4; l++) {
        int ii = i+xm[l];
        int jj = j+ym[l];
        if (OK(ii, jj)) {
            if (a[i][j] == a[ii][jj]) algfill(ii, jj);
        }
    }
}

int schimba (int i, int j) {
    int ii, jj, c, maxim = -1, sur;
    for (int l = 0; l < 4; l++) {
        sur = 0;
        c = a[ i+xm[l] ][ j+ym[l] ];

        for (int k = 0; k < 4; k++) {
            ii = i+xm[k];
            jj = j+ym[k];
            if (c == a[ii][jj] && !pa[ afill[ii][jj] ]) sur += b[ afill[ii][jj] ];

            pa[ afill[ii][jj] ] = 1;
        }

        for (int k = 0; k < 4; k++)
            pa[ afill[ i+xm[k] ][ j+ym[k] ] ] = 0;

        if (c != a[i][j])
            sur++;

        if (sur > maxim) maxim = sur, cul = c;
    }
    return maxim;
}

int main()
{
    char c;
    int v, i, j;
    fin >> v >> n >> m;
    for (i = 1; i <= n; i++) {
        for (j = 1; j <= m; j++) {
            fin >> c;
            a[i][j] = c-'a'+1;
        }
    }

    for (i = 1; i <= n; i++) {
        for (j = 1; j <= m; j++) {
            if (!afill[i][j]) {
                nr++;
                algfill(i, j);
            }
        }
    }

    if (v == 1) {
        int maxim=0;
        for (i = 1; i <= nr; i++)
            maxim = max(maxim, b[i]);
        fout << maxim;
        return 0;
    }

    for (i = 1; i <= n; i++) {
        for (j = 1; j <= m; j++) {
             int supr = schimba(i, j);
             if (supr > Max) {
                Max = supr;
                ip = i;
                jp = j;
                culoare = cul;
             }
        }
    }
    fout << ip << " " << jp << "\n" << char(culoare+ 'a'-1 );
    return 0;
}