Cel mai mare observator astronomic din România și din Europa de Est, aflat la Galați, a captat o imagine a boltei cerești, ce surprinde toate stelele vizibile în acel moment. Imaginea este în format digital, codificată sub forma unui tablou bidimensional, cu N linii și M coloane. Fiecare element al tabloului conține un număr natural care reprezintă intensitatea luminoasă a unei stele.
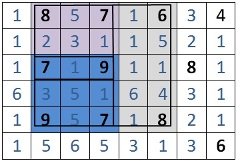
Numim stea strălucitoare o stea care are intensitatea luminoasă mai mare decât a tuturor stelelor învecinate direct cu ea, pe orizontală, verticală sau diagonală. Numim constelație pătrată patru stele strălucitoare care se află plasate în colțurile unui pătrat cu laturile paralele cu marginile tabloului. Lungimea laturii unei constelații pătrate este egală cu numărul de stele din care este formată latura. O stea strălucitoare poate face parte din mai multe constelații pătrate.
Cerințe
Scrieți un program care să determine:
a) Numărul stelelor strălucitoare;
b) Numărul constelațiilor pătrate;
c) Lungimea laturii pătratului care reprezintă cea mai mare constelație pătrată.
Date de intrare
Fișierul de intrare patrat2.in conține pe prima linie două numere naturale N și M, separate printr-un spațiu, reprezentând dimensiunile tabloului bidimensional, iar de pe următoarele N linii, câte M numere naturale separate prin câte un spațiu, reprezentând intensitatea luminoasă a stelelor.
Date de ieșire
Fișierul de ieșire patrat2.out va conține pe prima linie un număr natural reprezentând răspunsul la cerința a). Pe cea de-a doua linie se va scrie un număr natural reprezentând răspunsul la cerința b). Pe a treia linie se va scrie un număr natural reprezentând răspunsul la cerința c).
Restricții și precizări
1 < N ≤ 2001 < M ≤ 2001 ≤intensitatea unei stele≤ 1000- pentru rezolvarea corectă a cerinţei a) se acordă
40%din punctajul fiecărui test, pentru rezolvarea corectă a cerinţei b) se acordă40%din punctajul fiecărui test iar pentru rezolvarea corectă a cerinţei c) se acordă20%din punctajul fiecărui test.
Exemplul 1
patrat2.in
6 8 1 8 5 7 1 6 3 4 1 2 3 1 1 5 2 1 1 7 1 9 1 1 8 1 6 3 5 1 6 4 3 1 1 9 5 7 1 8 2 1 1 5 6 5 3 1 3 6
patrat2.out
11 3 5
Explicație
În tabloul bidimensional cu 6 linii și 8 coloane există 11 stele strălucitoare. Tabloul conține 3 constelații pătrate iar cea mai mare are latura pătratului de lungime 5.
Exemplul 2
patrat2.in
2 3 1 1 1 1 1 1
patrat2.out
0 0 0
Explicație
În tabloul bidimensional cu 2 linii și 3 coloane nu există nici o stele strălucitoare. Tabloul conține 0 constelații pătrate iar cea mai mare are latura pătratului de dimensiune 0.
SOLUTIE
#include <fstream>
#include <bitset>
using namespace std;
int mat[205][205];
bitset<205>mat2[205];
int di[8]= { -1,1,0,0,-1,-1,1,1 };
int dj[8]= { 0,0,-1,1,-1,1,-1,1 };
int main()
{ ifstream cin("patrat2.in");
ofstream cout("patrat2.out");
int n,m,cnt1=0,a,dist=1,cnt2=0,max=0,ok;
cin>>n>>m;
for(int i=1; i<=n; i++)
{
for(int j=1; j<=m; j++)
cin>>mat[i][j];
}
for(int i=1; i<=n; i++)
{
for(int j=1; j<=m; j++)
{
ok=0;
for(int k=0; k<8; k++)
{
ok=0;
if(mat[i][j]<=mat[i+di[k]][j+dj[k]])
{
ok=1;
break;
}
}
if(ok==0)
{
mat2[i][j]=1;
cnt1++;
}
}
}
cout<<cnt1<<'\n';
for(int i=1; i<=n; i++)
{
for(int j=1; j<=m; j++)
{
if(mat2[i][j]==1)
{
dist=1;
while(i+dist<=n&&j+dist<=m)
{
if(mat2[i][j+dist]==1&&mat2[i+dist][j]==1&&mat2[i+dist][j+dist]==1)
{
cnt2++;
if(dist+1>max)
max=dist+1;
}
dist++;
}
}
}
}
cout<<cnt2<<'\n'<<max;
return 0;
}