Definiţie: Un graf se numeşte graf conex dacă pentru oricare două vârfuri x şi y diferite ale sale, există un lanţ care le leagă, adică x este extremitatea iniţială şi y este extremitatea finală.
Un graf cu un singur nod este, prin definiţie, conex.
Definiţie: Se numeşte componentă conexă a unui graf G = (X,U) un subgraf H = (Y, V), conex, al lui G care are prorpietatea că nu există nici un lanţ în G care să lege un vârf din Y cu un vârf din X – Y.
Putem spune ca o componentă conexă a unui graf este un un subgraf conex şi maximal în raport cu această proprietate (nu există lanţ între un nod din subgraf şi un nod care nu aparţine subgrafului)
Un graf este conex dacă admite o singură componetă conexă.
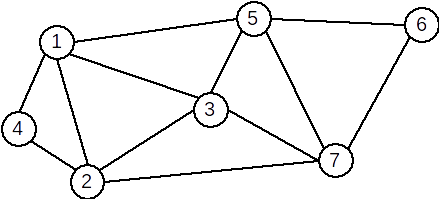
Exemplu: Graful de mai sus are o singură componentă conexă şi în consecinţă este conex.
In urmatorul exemplu exista 3 componente conexe

- G1 =(X1,U1), cu X1={1,2,3,4} şi U1={u1,u2,u3,u4}
- G2 =(X2,U2), cu X2={5,.6} şi U2={u5}
- G3 =(X3,U3), cu X3={7} şi U1= Ø
Observatie: Pentru a decide daca un graf este conex parcurgem graful pornind de la un nod. Daca se viziteaza toate nodurile atunci graful este conex.
Definiţie: Un graf este biconex dacâ este conex şi pentru orice vârf eliminat subgraful generat îşi păstrează proprietatea de conexitate
Exemplu: Graful definit mai jos este biconex.
