O fotografie alb-negru a surprins imaginea fulgerelor pe cerul întunecat în timpul unei furtuni electrice. Mărită, fotografia arată ca un caroiaj format din mici pătrate identice, albe sau negre, dispuse alăturat pe N rânduri și M coloane, câte M pe fiecare rând. Pătratele albe formează fulgerele din fotografie, iar pătratele negre reprezintă cerul. În fotografie, nu există două pătrate albe dispuse alăturat pe același rând. Un fulger este format din pătrate albe situate pe rânduri consecutive care respectă următoarele condiții: a) pătratele albe situate pe două rânduri consecutive au un vârf comun sau o latură comună; b) un fulger poate avea un singur pătrat alb pe un rând. În fotografie, fulgerele sunt distincte, ele neavând pătrate albe cu laturi sau vârfuri comune. Înălțimea unui fulger este dată de numărul de pătrate albe ale acelui fulger.
Pentru a putea fi analizată de către programatori, fotografia este codificată cu ajutorul unui tablou bidimensional cu N linii și M coloane, ale cărui elemente sunt 0 și 1. Valoarea 0 este codificarea pătratului negru, iar valoarea 1 este codificarea pătratului alb.
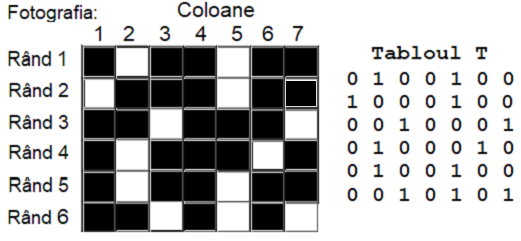
Având codificarea, programatorii trebuie să găsească numărul maxim P de pătrate negre dispuse alăturat pe același rând, numărul de fulgere F precum și înălțimea maximă H a unui fulger din fotografie. De exemplu, fotografia de mai jos este codificată de tabloul T alăturat fotografiei .
Cerința
Scrieți un program care citește numerele N și M, cele N*M elemente ale tabloului T care codifică fotografia și rezolvă următoarele cerințe:
- afișează numărul maxim
Pde pătrate negre dispuse alăturat pe un rând în fotografie; - afișează numărul
Fde fulgere și înălțimea maximăHa unui fulger din fotografie.
Date de intrare
Fișierul de intrare foto.in conține pe prima linie un număr natural C reprezentând cerința care trebuie rezolvată (1 sau 2). Pe a doua linie se află cele două numere naturale N și M, separate printr-un spațiu, cu semnificația din enunț. Pe fiecare dintre următoarele N linii se află câte M valori 0 sau 1, separate prin câte un spațiu, reprezentând elementele tabloului care codifică fotografia, în ordinea parcurgerii lor pe rânduri, de sus în jos, și de la stânga la dreapta în cadrul unui rând.
Date de ieșire
Fișierul de ieșire foto.out va conține, pe o singură linie:
- dacă
C=1, numărulP, reprezentând răspunsul la cerința1; - dacă
C=2, cele două numereFșiH, în această ordine, separate printr-un singur spațiu, reprezentând
răspunsul la cerinţa2.
Restricții și precizări
Nnumăr natural,4 ≤ N ≤ 100Mnumăr natural,4 ≤ M ≤ 100- În concurs, pentru rezolvarea cerinței
1s-au acordat 20 de puncte, pentru rezolvarea cerinței2s-au acordat 70 de puncte. Pe site se acordă 10 puncte pentru exemple.
Exemplul 1
foto.in
1 6 7 0 1 0 0 1 0 0 1 0 0 0 1 0 0 0 0 1 0 0 0 1 0 1 0 0 0 1 0 0 1 0 0 1 0 0 0 0 1 0 1 0 1
foto.out
3
Explicație
Se rezolvă cerința 1. N=6, M=7. Sunt maximum P=3 pătrate negre alăturate pe rândurile 2, 3 și 4 (vezi fotografia din enunț).
Exemplul 2
foto.in
2 6 7 0 1 0 0 1 0 0 1 0 0 0 1 0 0 0 0 1 0 0 0 1 0 1 0 0 0 1 0 0 1 0 0 1 0 0 0 0 1 0 1 0 1
foto.out
5 4
Explicație
Se rezolvă cerința 2. N=6, M=7. Sunt F=5 fulgere iar înălțimea maximă a unui fulger este H=4 (vezi fotografia din enunț).
#include <fstream>
using namespace std;
bool mat[105][105];
int main()
{
ifstream cin("foto.in");
ofstream cout("foto.out");
int cnt=0,maxcnt=0,a,b,cer,inalt=0;
cin>>cer>>a>>b;
for(int i=1; i<=a; i++)
{
for(int j=1; j<=b; j++)
{
cin>>mat[i][j];
if(mat[i][j]==0)
{
cnt++;
}
else
{
if(cnt>maxcnt)
maxcnt=cnt;
cnt=0;
}
}
if(cnt>maxcnt)
maxcnt=cnt;
cnt=0;
}
if(cer==1)
cout<<maxcnt;
else
{
int maxinalt,fulger,poz1,poz2;
maxinalt=fulger=0;
for(int i=1; i<=a; i++)
{
for(int j=1; j<=b; j++)
{
if(mat[i][j]==1)
{
fulger++;
mat[i][j]=0;
poz1=i;
poz2=j;
while(1)
{
mat[poz1][poz2]=0;inalt++;
if(mat[poz1+1][poz2+1]==1){poz1++;poz2++;}
else if(mat[poz1+1][poz2-1]==1){poz1++;poz2--;}
else if(mat[poz1+1][poz2]==1){poz1++;}
else break;
}
if(inalt>maxinalt) maxinalt=inalt;
inalt=0;
}
}
}
cout<<fulger<<" "<<maxinalt;
}
return 0;
}